基于绝热逻辑的低功耗乘法器电路设计方案

过去的40年中，MOS器件尺寸的持续缩小一直是促进半导体工业发展的动力。人们可以在越来越小的芯片上实现越来越复杂的功能，并且芯片的价格不断下降，使得各种便携式产品如笔记本电脑、笔迹识别仪、语音识别器等相继问世。这些设备大多依靠电池供电，电池的寿命是有限的，而目前的镍镉电池最多能提供的电能只有 26 W／pound。而且，随着芯片集成度的增加，单位面积上消耗的功率也随之增加，这不得不增加为芯片散热的成本。因而，如文献中所述，电路的低功耗已成为电路设计的重要指标。

从已有的研究成果可知，电路中的功率消耗源主要有以下几种：由逻辑转换引起的逻辑门对负载电容充、放电引起的功率消耗；由逻辑门中瞬时短路电流引起的功率消耗；由器件的漏电流引起的消耗，并且每引进一次新的制造技术会导致漏电流20倍的增加，漏电流引起的消耗已经成为功率消耗的主要因素。目前降低功耗的方法主要有：减小电源电压、调整晶体管尺寸、采用并行和流水线的系统结构、利用睡眠模式、采用绝热逻辑电路等。其中，能量回收逻辑就是基于绝热计算发展起来的一种低功耗设计技术。这里简单介绍一种使用单相正弦电源时钟的能量回收逻辑，并用这种原理电路设计了一个两位的数字乘法器电路，与静态CMOS数字乘法器相比，这种能量回收乘法器能够大大降低功率消耗。

1 单相正弦电源时钟能量回收逻辑电路工作原理

以反相器为例说明这种电路的工作原理，如图1所示。M1和M2的连接方式与传统的静态CMOS逻辑电路相似。不同的是电源不再是恒定不变的，而是用一个正弦信号代替，这个信号同时起到同步电路工作的作用，因此又称作电源时钟。M3和M4连接成二极管的形式用来控制充放电的路径。

当输入信号B为逻辑“O”时，M1导通，M2截止。正弦信号正半周时，通过M3和M1向负载电容充电，一旦电容充电到最大值，M3能够阻止电容向输入正弦时钟信号放电，输出保持在高电平不变。当输入信号B为逻辑“1”时，M1截止，M2导通。正弦信号负半周时，负载电容通过M2和M4向输入正弦时钟信号放电，一旦电容放电到最小值，M4能够阻止输入正弦时钟信号向电容充电，输出保持为低电平不变。

2 基于单相能量回收电路的乘法器电路设计

2．1 基于单相能量回收电路的乘法器

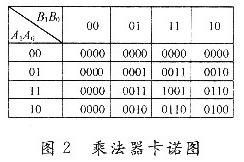
两位乘法器能够实现2位二进制数的乘法运算，设A1A0，B1B0为乘数和被乘数，P3P2P1P0为乘法运算得到的积，由卡诺图(见图2)得到两位乘法器的输出逻辑函数表达式分别为：

为了能用基本的与非门、或非门和异或门电路实现乘法器，上式可以通过逻辑运算变换为：

实现电路时，将静态CMOS电路(见图3)构成的与非门、或非门和异或门的电源用图4所示的电源时钟电路代替即可。其中Clk+，Clk-分别接CMOS电路中PMOS和NMOS管的D极和S极。

2．2 仿真结果

在PSpice环境下，分别仿真了用静态CMOS电路和单相能量回收电路构成的两位乘法器电路(见图5和图6)，图中只显示了输出4位积的低2位P1P0，其中输入信号 A1A0，B1B0波形见图6。其他参数如下：采用CMOS 1．2μm技术，正弦波峰峰值为2．5 V，直流电压VDD为2．5 V，并假设乘法器的输出端接负载电容为O．1 fF。

从图中可见，用静态CMOS电路构成的乘法器输出比较稳定，输出等于0或VDD，功率消耗为1．51×10-7W。而用单相能量回收电路构成的二位乘法器的输出不够稳定，对噪声信号较为敏感，但是并不影响输出逻辑，功率消耗减小为1．17×10-7W。从节能的角度来看，单相能量回收电路性能更好。

3 结语

本文首先介绍了单相能量回收反相器电路，详细讨论电路的工作原理，同时用PSpice工具仿真了基于静态CMOS电路和单相能量回收电路构成的两位乘法器电路。仿真结果表明本文介绍的单相能量回收电路能够极大地降低电路功耗。今后的工作还应继续优化电路结构，稳定电路的输出状态，增强电路的抗干扰能力。